最小生成树算法

1. 概念

1.1 生成树

• 若图是【连通的无向图】或【强连通的有向图】，则从其中任一顶点出发，调用一次 dfs 或者 bfs 后，可以系统的访问图中所有顶点。
• 若图是【有根的有向图】 ，则从根出发，调用一次 dfs 或者 bfs 后，可以系统的访问图中所有顶点。

在上述情况之下，图中所有顶点加上遍历过程中经过的所有边所构成的子图称为原图的生成树。

若图是不连通的的无向图和不是强连通的有向图，从其中任一顶点出发，调用一次 dfs 或者 bfs 后，不能访问到图中所有顶点，只能得到以出发点为根的连通分支（或者强连通分支）的生成树。若想访问其他顶点则需要以一个没有访问过的点作为起点，再次调用 dfs 或者 bfs，这样就得到了生成森林。

很显然，一个图的生成树并不是唯一的，不同的搜索方法或者同一个搜索方法但出发点不同，都可以得到不同的生成树。

可以证明：具有 n 个顶点的图，其对应的生成树有 n-1 条边。

1.2 加权图

加权图是一种为每条边关联一个权值或是成本的图。这种图能够自然地表示许多应用。在一幅航空图中，边表示航线，权值则可以表示距离或是费用。在一幅电路图中，边表示导线，权值则可能表示导线的长度即成本，或是信号通过这条线路所需的时间。在这些情形中，最令人感兴趣的自然是将成本最小化。

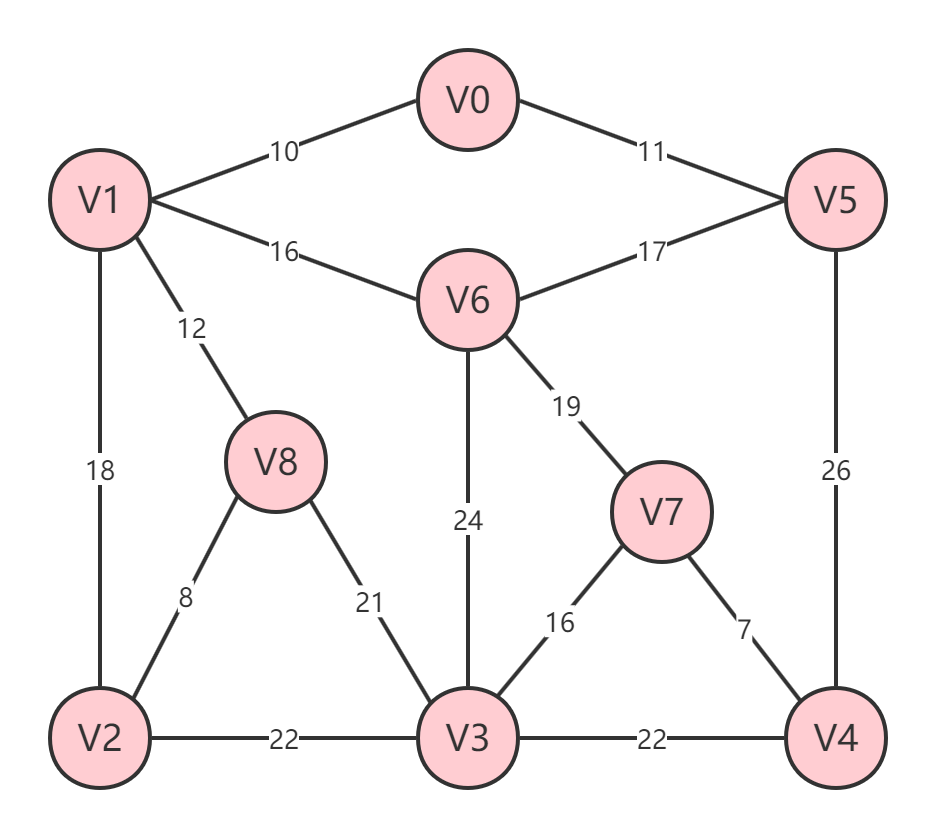
1.3 最小生成树

图的生成树是它的一棵含有其所有顶点的无环连通子图。一幅加权图的最小生成树（Minimum Spanning Tree, MST）是它的一棵权值（树中所有边的权值之和）最小的生成树。

将上面的加权图转换为最小生成树为：

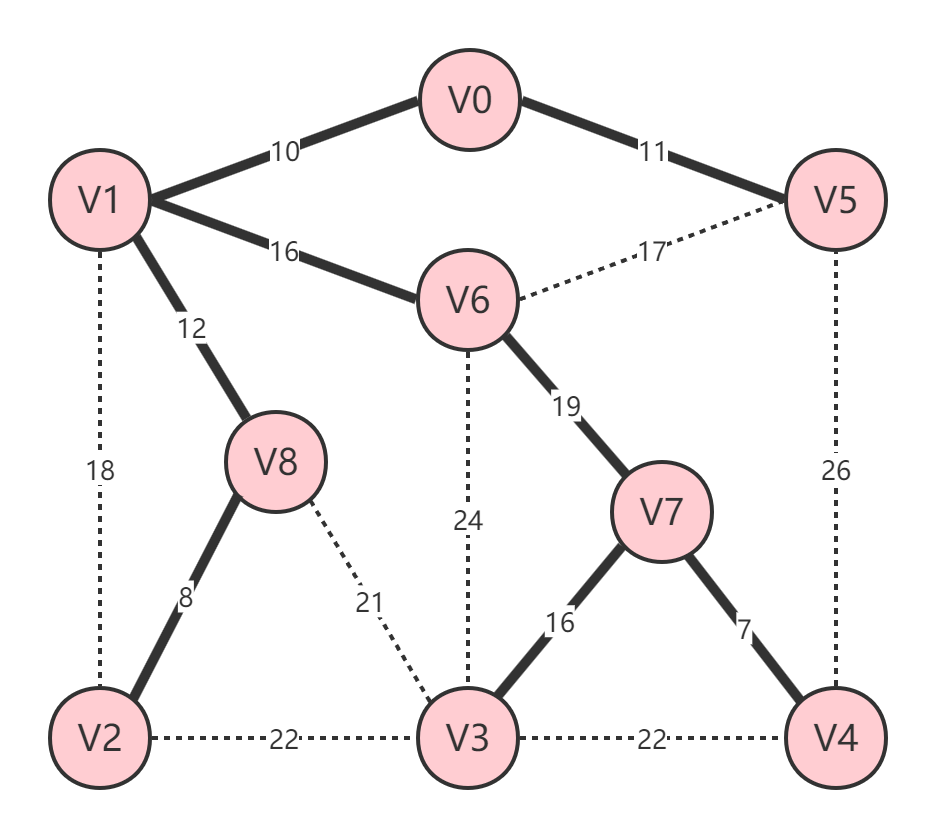
2. 算法

2.1 普利姆算法

2.1.1 思想

1. 任选一个点作为起始点，将其加入到生成树当中。

2. 从起始点出发，首先考虑他所能到达的所有点的集合 next，从中选择最近的一个点加入到生成树中，此时生成树中有两个点，更新所能到达点的集合 next。

3. 从集合 next 中选择还未去过且最近的点加入到生成树中，并更新 next，重复此步骤直到所有节点到加入到生成树当中。

整体来说就是贪心算法，每走一步都求出该步的最优解。

以上面介绍的加权图为例，它的生成过程为：

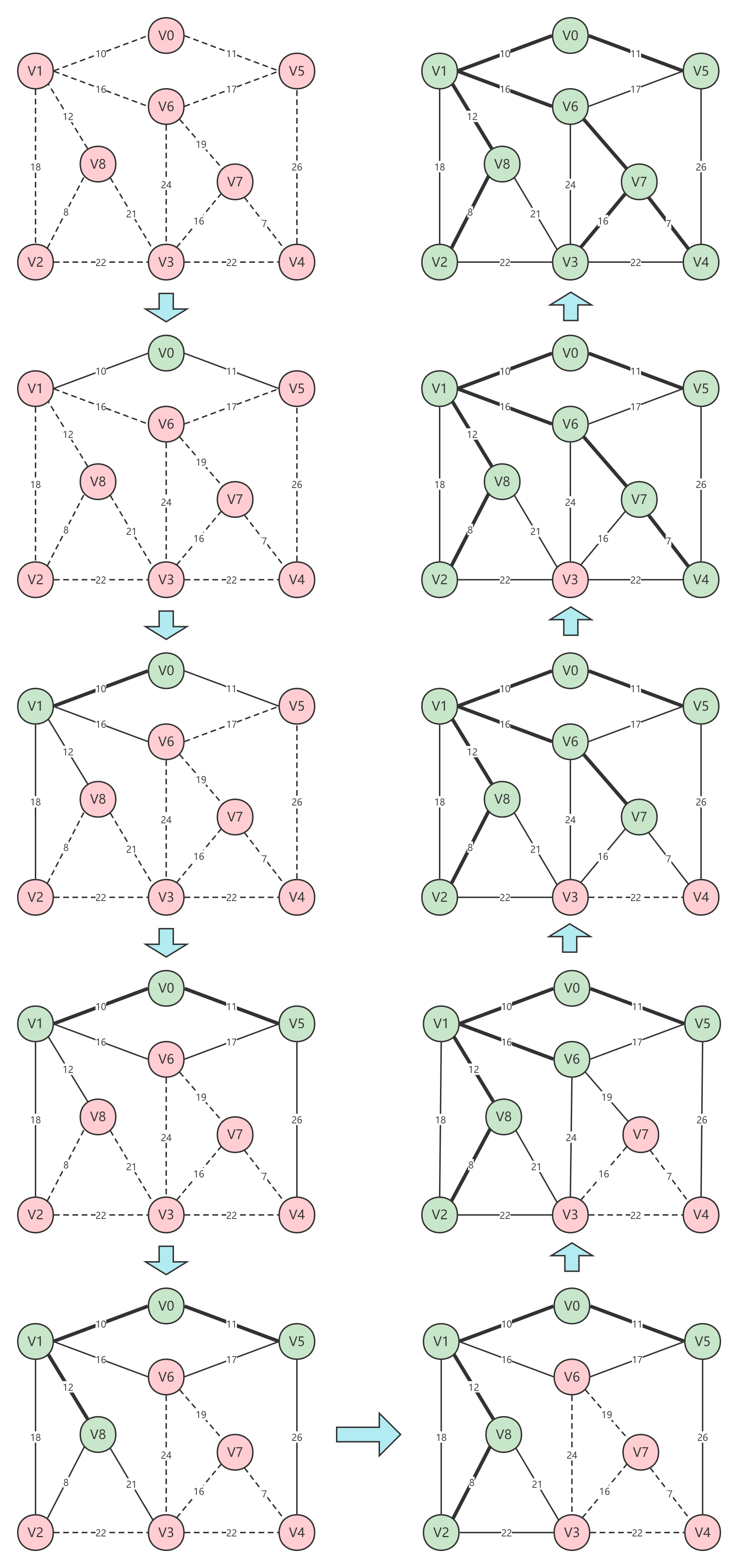
2.1.2 代码

public class MST {
    public static void main(String[] args) {
        final int MAX = Integer.MAX_VALUE;
        MST mst = new MST();
        // 上图所构建的邻接矩阵
        int[][] g = {
                {0,     10,     MAX,    MAX,    MAX,    11,     MAX,    MAX,    MAX},
                {10,    0,      18,     MAX,    MAX,    MAX,    16,     MAX,    12},
                {MAX,   18,     0,      22,     MAX,    MAX,    MAX,    MAX,    8},
                {MAX,   MAX,    22,     0,      20,     MAX,    24,     16,     21},
                {MAX,   MAX,    MAX,    20,     0,      26,     MAX,    7,      MAX},
                {11,    MAX,    MAX,    MAX,    26,     0,      17,     MAX,    MAX},
                {MAX,   16,     MAX,    24,     MAX,    17,     0,      19,     MAX},
                {MAX,   MAX,    MAX,    16,     7,      MAX,    19,     0,      MAX},
                {MAX,   12,     8,      21,     MAX,    MAX,    MAX,    MAX,    0}
        };
        mst.prim(g);
    }

    /**
     * 普利姆Prim算法
     * @param adjacencyMatrix 邻接矩阵，表示两点间距离，Integer.MAX_VALUE：表示两个点无法到达
     */
    public int prim(int[][] adjacencyMatrix) {
        // 一共n个点
        int n = adjacencyMatrix.length;
        // 【轨迹数组】到达该索引位置最近的点,用于记录轨迹
        int[] route = new int[n];
        // 【可达点数组】已到达顶点值为0，无法达到顶点值为Integer.MAX_VALUE，否则，为可探索的点和到这些点的距离（权值）
        int[] distance = new int[n];
        // 最短路径和
        int sum = 0;
        // 初始化distance，假设起始点是0，也就是第0个点可到达的点。
        for (int i = 0; i < n; i++) {
            distance[i] = adjacencyMatrix[0][i];
        }
        // 从第一行遍历邻接矩阵
        for (int i = 1; i < n; i++) {
            int min = Integer.MAX_VALUE;
            int nextIndex = 0;
            // 遍历当前所有节点，寻找可到达点中，最近的点nextIndex及其距离min
            for (int j = 0; j < n; j++) {
                if (distance[j] != 0 && distance[j] < min) {
                    min = distance[j];
                    nextIndex = j;
                }
            }
            System.out.println("最近的节点为：" + nextIndex + ", 距离为：" + min);
            // 将该点纳入最小生成树当中
            sum += distance[nextIndex];
            distance[nextIndex] = 0;

            // 通过点nextIndex更新可达点数组distance
            for (int j = 1; j < n; j++) {
                if (distance[j] != 0 && adjacencyMatrix[nextIndex][j] < distance[j]) {
                    // 更新distance不为0和MAX的距离，添加一些可以新达到点的距离。
                    distance[j] = adjacencyMatrix[nextIndex][j];
                    // 能到达这些新点的顶点只有nextIndex
                    route[j] = nextIndex;
                }
            }
        }
        return sum;
    }
}

时间复杂度：O(n²)

2.2 库鲁斯卡尔算法

// TODO