最短路径算法

1. 概述

对于加权图来说，最短路径是指两顶点之间经过的边上权值之和最小的路径，并且我们称路径上的第一个顶点是源点，最后一个点是终点。

以下面这副加权图为例：

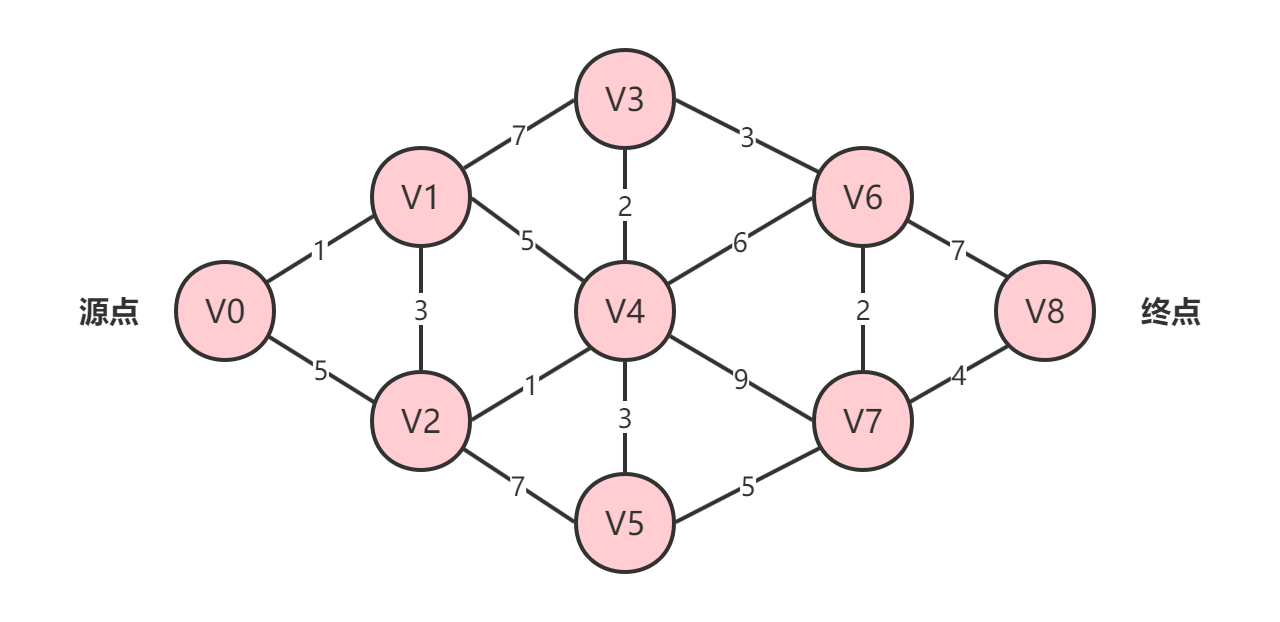
其最短路径为：

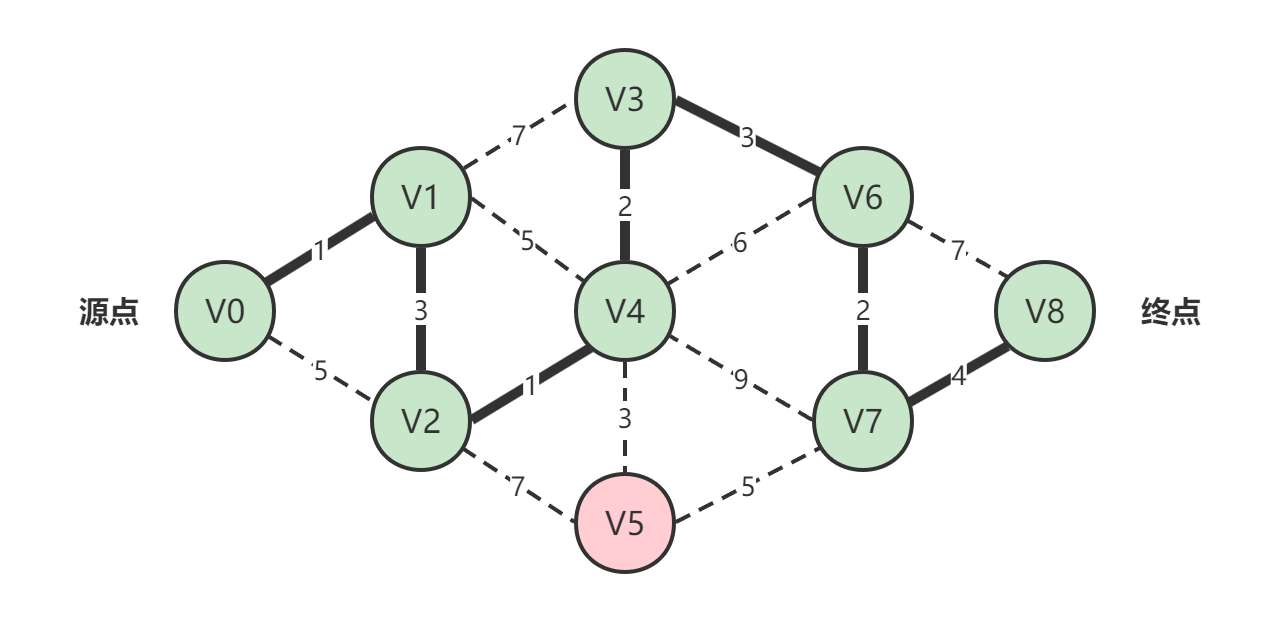
2. 算法

2.1 迪杰斯特拉算法

迪科斯彻算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题，算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。

时间复杂度：O(n²)

public class Dijkstra {
    private static final int INF = Integer.MAX_VALUE;

    /**
     *
     * @param graph 图
     * @param source 起点
     */
    public static void dijkstra(int[][] graph, int source) {
        // 顶点数量
        int vertices = graph.length;
        // 从起点出发到达某一个点的最短距离
        int[] dist = new int[vertices];
        boolean[] visited = new boolean[vertices];

        // 初始化距离数组
        Arrays.fill(dist, INF);
        dist[source] = 0;

        for (int i = 0; i < vertices - 1; i++) {
            int minDist = INF;
            int minIndex = -1;

            // 选择距离最小的顶点
            for (int j = 0; j < vertices; j++) {
                if (!visited[j] && dist[j] < minDist) {
                    minDist = dist[j];
                    minIndex = j;
                }
            }

            // 标记该顶点为已访问
            visited[minIndex] = true;

            // 更新与该顶点相邻顶点的最短距离
            for (int j = 0; j < vertices; j++) {
                if (!visited[j] && graph[minIndex][j] != 0 && dist[minIndex] != INF) {
                    dist[j] = Math.min(dist[j], dist[minIndex] + graph[minIndex][j]);
                }
            }
        }

        // 打印最短路径
        printShortestPaths(dist);
    }

    public static void printShortestPaths(int[] dist) {
        int vertices = dist.length;
        System.out.println("顶点\t\t最短距离");
        for (int i = 0; i < vertices; i++) {
            System.out.println(i + "\t\t" + dist[i]);
        }
    }

    public static void main(String[] args) {
        int[][] graph = {
                {0, 1, 5, 0, 0, 0, 0, 0, 0},
                {1, 0, 3, 7, 5, 0, 0, 0, 0},
                {5, 3, 0, 0, 1, 7, 0, 0, 0},
                {0, 7, 0, 0, 2, 0, 3, 0, 0},
                {0, 5, 1, 2, 0, 3, 6, 9, 0},
                {0, 0, 7, 0, 3, 0, 0, 5, 0},
                {0, 0, 0, 3, 6, 0, 0, 2, 7},
                {0, 0, 0, 0, 9, 5, 2, 0, 4},
                {0, 0, 0, 0, 0, 0, 7, 4, 0}
        };

        dijkstra(graph, 0);
    }
}

2.2 弗洛伊德算法

// TODO